A módusz kiszámítása a statisztika egyik legegyszerűbb, mégis gyakran félreértett művelete. A módusz azt mutatja meg, melyik érték fordul elő leggyakrabban egy adathalmazban. Nem átlagról, nem középről, hanem gyakoriságról van szó – ezért különösen hasznos, ha szeretnéd megtudni, mi a legjellemzőbb adat egy csoportban.
Ebben a cikkben megmutatom, mit jelent pontosan a módusz, hogyan számítható ki kézzel, táblázatból vagy Excelben, és mikor érdemes használni az átlag, medián helyett (vagy mellett).
Mi az a módusz?
A módusz (jelölése: Mo) az az érték, amely legtöbbször előfordul az adathalmazban.
Más szóval: ha egy adat többször szerepel, mint a többi, akkor ő lesz a módusz.
Példa:
Adatsor: 4, 5, 5, 7, 8, 8, 8, 9
→ A módusz = 8, mert az fordul elő legtöbbször (háromszor).
Ha minden érték egyszer szerepel, nincs módusz.
Ha több érték azonos gyakorisággal szerepel, akkor többmóduszú (bimodális vagy multimodális) az adatsor.
Mikor érdemes a móduszt használni?
A módusz kiszámítása különösen hasznos, ha kategóriás vagy diszkrét adatokkal dolgozol – például:
Nem érzékeny a szélsőséges értékekre, ezért jól használható torz eloszlások esetén is.
A módusz kiszámítása lépésről lépésre
1. Gyűjtsd össze az adatokat
Például: 2, 3, 3, 5, 5, 5, 7, 8, 8
2. Csoportosítsd, és számold meg, melyik hányszor fordul elő
| Érték | Gyakoriság |
|---|---|
| 2 | 1 |
| 3 | 2 |
| 5 | 3 |
| 7 | 1 |
| 8 | 2 |
3. A legnagyobb gyakorisághoz tartozó érték a módusz
Itt: 5, mert háromszor fordul elő.
👉 Módusz = 5
Különleges esetek
Példa:
Adatsor: 3, 3, 4, 4, 5, 6
→ Két módusz van: 3 és 4 → az adatsor bimodális.
A módusz kiszámítása Excelben
Az Excel és a Google Táblázatok is ismerik a módusz függvényt.
Alapfüggvény:
=MÓDUSZ.EGY(A1:A10)
– az első leggyakoribb értéket adja vissza.
Ha több módusz is van, használhatod:
=MÓDUSZ.TÖBB(A1:A10)
– többértékű tömböt ad vissza (ha több azonos gyakoriságú adat van).
Csoportosított adatok esetén
Ha az adatokat osztályokba (intervallumokba) rendezted, a módusz közelítő képlete a következő:
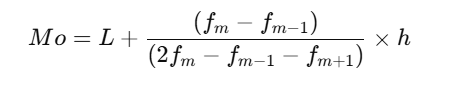
ahol:
Ez a képlet a statisztikai elemzésekben (pl. demográfiai, piackutatási adatoknál) használatos, ahol az adatok intervallumokra vannak bontva.
Módusz, medián és átlag összehasonlítása
| Mutató | Jelentése | Mikor használjuk | Szélsőséges értékekre érzékeny? |
|---|---|---|---|
| Átlag | Összes érték átlaga | Szimmetrikus eloszlásnál | Igen |
| Medián | Középső érték | Torz eloszlásnál | Nem |
| Módusz | Leggyakoribb érték | Kategóriás, diszkrét adatoknál | Nem |
Gyakorlati példák
1. példa – Iskolai jegyek
Jegyek: 2, 3, 3, 4, 4, 4, 5
→ A legtöbbször a 4-es szerepel → Módusz = 4
2. példa – Cipőméretek
Méretadatok: 39, 40, 40, 41, 41, 41, 42
→ A 41-es méret a leggyakoribb → Módusz = 41
3. példa – Többmóduszú eloszlás
Adatsor: 1, 2, 2, 3, 3, 4
→ Két leggyakoribb érték: 2 és 3 → Bimodális adatsor.
Összefoglalás
A módusz kiszámítása a legegyszerűbb módja annak, hogy megtudd, mi a leggyakrabban előforduló érték az adataidban.
Nem igényel bonyolult képleteket, csak gyakoriság-számlálást.
Ha több adat azonos gyakorisággal szerepel, a sorozat lehet többmóduszú is.
Egy jól kiválasztott statisztikai mutató – akár az átlag, medián, akár a módusz – segít abban, hogy pontosabb képet kapj a vizsgált adathalmazról.

