A legkisebb közös többszörös kiszámítása (röviden LKT vagy angolul LCM – Least Common Multiple) az egyik alapvető művelet a matematika világában. Hasznos nemcsak az iskolai feladatokban, hanem a mindennapokban is – például ha két ismétlődő esemény közös időpontját keresed, vagy törteket akarsz közös nevezőre hozni. Nézzük meg lépésről lépésre, hogyan működik a számítás.
Mi az a legkisebb közös többszörös?
A legkisebb közös többszörös két vagy több számnak az a legkisebb pozitív szám, amely mindegyikkel osztható.
Például:
A legkisebb közös többszörös kiszámítása többféleképpen
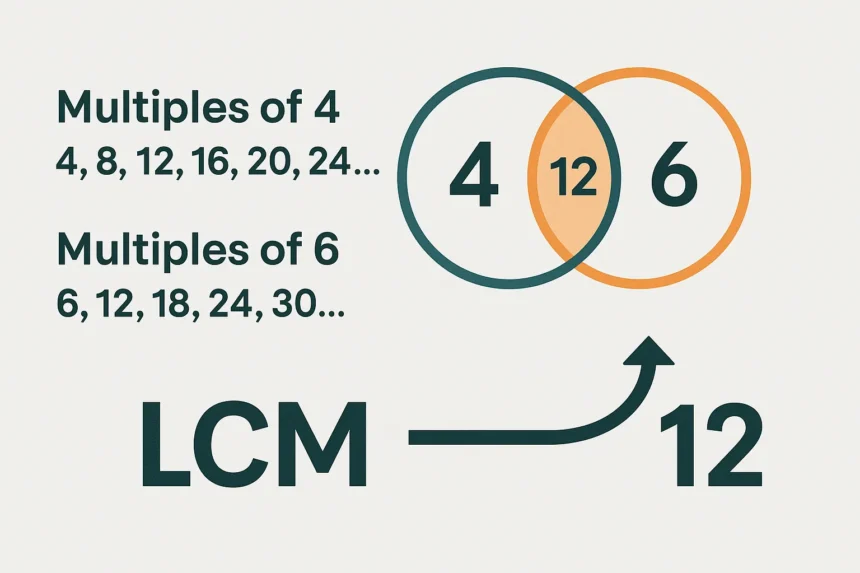
1. módszer: többszörösök felsorolása (alap szint)
Ez a legegyszerűbb, de nagyobb számoknál időigényes.
Lépések:
Példa:
12 és 18 többszörösei:
2. Módszer: prímtényezős felbontás (rendszeres módszer)
A legkisebb közös többszörös kiszámítása a prímtényezős felbontással a leggyorsabb, ha pontosan akarunk dolgozni.
Lépések:
Példa:
12 = 2² × 3
18 = 2 × 3²
→ minden prímből a legnagyobb hatvány: 2² és 3²
LKT = 2² × 3² = 4 × 9 = 36
3. Módszer: legnagyobb közös osztó segítségével (haladó)
Használhatjuk a következő képletet is, amely gyorsabb nagy számok esetén:
LKT(a, b) = (a × b) / LNKO(a, b)
ahol LNKO = legnagyobb közös osztó.
Példa:
a = 20, b = 30
LNKO(20, 30) = 10
LKT = (20 × 30) / 10 = 600 / 10 = 60
Eredmény: LKT(20, 30) = 60
4. Módszer: több szám esetén
Ha három vagy több számmal dolgozol, a módszer ugyanaz:
LKT(a, b, c) = LKT(LKT(a, b), c)
Példa:
LKT(6, 8, 10)
Először LKT(6, 8) = 24
Majd LKT(24, 10) = 120
Eredmény: LKT(6, 8, 10) = 120
Gyakorlati példák
Példa 1 – közös nevezőre hozás
Ha két törted van:
1/6 + 1/8
A nevezők legkisebb közös többszöröse: LKT(6, 8) = 24
→ Közös nevező: 24
1/6 = 4/24
1/8 = 3/24
Összeg = 7/24
Példa 2 – valós életbeli feladat
Egy busz 12 percenként, egy villamos 18 percenként indul. Mikor indulnak újra egyszerre?
LKT(12, 18) = 36
→ 36 perc múlva találkoznak újra.
Tippek a gyors számításhoz
Ha a két szám egymás többszöröse, akkor a nagyobbik szám az LKT.
Ha a két szám prím egymáshoz képest, akkor az LKT = a × b.
Kombináld a LNKO képletet nagyobb számokhoz, mert sokkal gyorsabb, mint a felsorolás.
Összefoglalás
A legkisebb közös többszörös kiszámítása egyszerű, ha ismered a módszert.